问题
证明题
已知函数y=f(x)的定义域为R,且对任意a,b∈R,都有f(a+b)= f(a)+ f(b),且当x>0时,f(x)<0恒成立,证明:
(1)函数y=f(x)是R上的减函数;
(2)函数y=f(x)是奇函数。
答案
证明:(1)设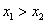 ,则
,则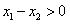 ,
,
又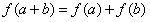 ,
,
∴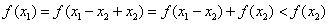 ,
,
∴函数 是R上的减函数。
是R上的减函数。
(2)由 ,得
,得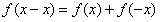 ,
,
即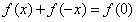 ,
,
又 ,
,
∴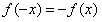 ,
,
即函数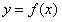 是奇函数。
是奇函数。
已知函数y=f(x)的定义域为R,且对任意a,b∈R,都有f(a+b)= f(a)+ f(b),且当x>0时,f(x)<0恒成立,证明:
(1)函数y=f(x)是R上的减函数;
(2)函数y=f(x)是奇函数。
证明:(1)设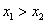 ,则
,则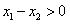 ,
,
又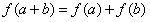 ,
,
∴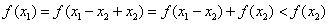 ,
,
∴函数 是R上的减函数。
是R上的减函数。
(2)由 ,得
,得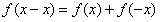 ,
,
即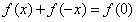 ,
,
又 ,
,
∴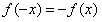 ,
,
即函数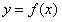 是奇函数。
是奇函数。