问题
解答题
抛物线的顶点是双曲线16x2-9y2=144的中心,而焦点是双曲线的左顶点,求抛物线的方程.
答案
抛物线方程为y2=-12x.
双曲线方程化为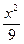
-
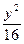=1.
其中心为(0,0),左顶点为F(-3,0).
设抛物线方程为y2=-2px(p>0),则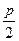
=3.
∴p=6.∴所求抛物线方程为y2=-12x.
搜题请搜索小程序“爱下问搜题”
抛物线的顶点是双曲线16x2-9y2=144的中心,而焦点是双曲线的左顶点,求抛物线的方程.
抛物线方程为y2=-12x.
双曲线方程化为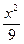-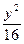=1.
其中心为(0,0),左顶点为F(-3,0).
设抛物线方程为y2=-2px(p>0),则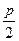=3.
∴p=6.∴所求抛物线方程为y2=-12x.