问题
填空题
设函数f(x)=|3x-1|的定义域是[a,b],值域是[2a,2b] (b>a),则a+b= .
答案
1
因为f(x)=|3x-1|的值域为[2a,2b],
所以b>a≥0,
而函数f(x)=|3x-1|在[0,+∞)上是单调递增函数,
因此应有 ,解得
,解得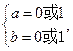 ∵
∵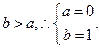
所以有a+b=1.
设函数f(x)=|3x-1|的定义域是[a,b],值域是[2a,2b] (b>a),则a+b= .
1
因为f(x)=|3x-1|的值域为[2a,2b],
所以b>a≥0,
而函数f(x)=|3x-1|在[0,+∞)上是单调递增函数,
因此应有 ,解得
,解得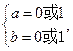 ∵
∵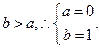
所以有a+b=1.