问题
问答题
设
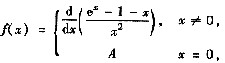
(Ⅰ)求常数A,使f(x)在(-∞,+∞)任意阶可导并求f(x)在x=0处的幂级数展开;
(Ⅱ) 求f(n)(0)(n=1,2,3,…).
答案
参考答案:[分析与求解] (Ⅰ)由ex的幂级数展开式可得
[*]
(x∈(-∞,+∞),x≠0),注意上式右端幂级数当x=0时取值为[*]
[*]
对g(x)逐项求导得
[*]
因此,[*]时f(x)在(-∞,+∞)可展成幂级数
[*]
因为幂级数在收敛区间内任意次可导,所以f(x)在(-∞,+∞)内任意次可导.
(Ⅱ)由幂级数展开式的唯一性[*]则
f(n)(0)=n!an.
因此[*]