证明下列结论：
(Ⅰ)设f’(x0)=0，f"(x0)＞0，则存在δ＞>0使得y=f(x)在(x0-δ，x0]单调减少，在[x0，x0+δ)单调增加；
(Ⅱ)设f(x)在[0，1]连续，在(0，1)二阶可导且f(0)=f(1)=0，f"(x)＜0(x∈(0，1))，则f(x)＞0(x∈(0，1))．又设
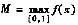，则存在唯一的ξ∈(0，1)，使得f’(ξ)=M．
参考答案：[分析与证明] (Ⅰ)由二阶导数定义
[*]
及极限的不等式性质[*][*]δ＞0，当x∈(x0-δ，x0+δ)且x≠x0时[*]
[*]
(Ⅱ)由假设条件及罗尔定理，[*]a∈(0，1)，f’(a)=0．由f’(x)在[*]
[*]
[*]
下证另一结论．
[*]
方法1° 要证：f’(x)-M在(0，1)3零点[*][f(x)-Mx]’在(0，1)[*]零点．
作辅助函数[*]在[0，1]连续，在(0，1)可导，F(0)=f(0)=0．再找F(x)在(0，1)的一个零点．由
F(0)=f(0)-Ma=M(1-a)＞0，
F(1)=f(1)-M=-M＜0
[*]，使得F(η)=0．
在[0，η]∈[0，1]上对F(x)用罗尔定理：[*]使得F’(ξ)=0，即
f’(ξ)=M．
方法2° 同前分析，作辅助函数
F(x)=f(x)-Mx，
F(x)在[0，1]连续，在(0，1)可导，且
F(0)=0，F(a)=M(1-0)＞0，F(1)=-M＜0
[*]F(x)在[0，1]的最大值不能在x=0或x=1取到[*]使得[*]由费马定理[*]即f’(ξ)=M．
方法3° 先证M是f’(x)的某一中间值．由[*]
又由拉格朗日中值定理，[*]使得
[*]
亦即 f’(0)＜M＜f’(η)．
由连续函数中间值定理[*]使得f’(ξ)=M．
最后证唯一性．由[*]
f’(ξ)=M．