问题
问答题
假定甲、乙两项资产的历史收益率的有关资料如下表：
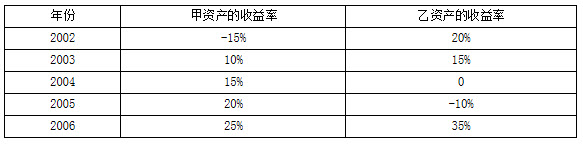
要求：
(1)分别计算甲、乙两项资产的期望收益率；
(2)分别计算甲、乙两项资产收益率的标准差；
(3)分别计算甲、乙两项资产收益率的变化系数；
(4)假设资本资产定价模型成立，无风险报酬率为5%，股票市场的平均收益率为 15%，分别计算甲、乙两项资产的β值；
(5)假设股票市场收益率的标准差为15%，分别计算甲、乙两项资产收益率与市场组合收益率的相关系数；
(6)假设按照40%和60%的比例购买甲、乙两项资产构成投资组合，计算该组合的综合β值和组合的投资收益率。
答案
参考答案：
(1)计算甲、乙两项资产的期望收益率：
甲资产的期望收益率=(-15%+10%+15%+20%+25%)/5=11%
乙资产的期望收益率=(20%+15%+0-10%+35%)/5=12%
(2)计算甲、乙两项资产收益率的标准差：
甲资产收益率的标准差=
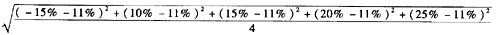
=15.57%
乙资产收益率的标准差=
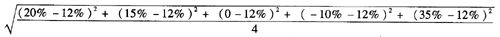
=17.54%
(3)计算甲、乙两项资产收益率的变化系数：
甲资产收益率的变化系数=15.57%/11%=1.42
乙资产收益率的变化系数=17.54%/12%=1.46
(4)计算甲、乙两项资产的β值：
11%=5%+β甲(15%-5%)，则β甲=0.6
12%=5%+β乙(15%-5%)，则β乙=0.7
(5)计算甲、乙两项资产收益率与市场组合收益率的相关系数：
根据βJ=rJM× 
，则rJM=βJ× 
甲资产收益率与市场组合收益率的相关系数=0.6× 
=0.578
乙资产收益率与市场组合收益率的相关系数=0.7×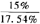 
=0.599
(6)计算该组合的综合β值和组合的投资收益率：
组合的综合β值=40%×0.6+60%×0.7=0.66
组合的投资收益率=40%×11%+60%×12%=11.6%。