问题
解答题
已知抛物线y2=x上存在两点关于直线l:y=k(x-1)+1对称,求实数k的取值范围.
答案
-2<k<0即为所求.
解法一:设抛物线上的点A(x1,y1)、B(x2,y2)关于直线l对称,则y12=x1,y22=x2.
两式相减得(y1+y2)·(y1-y2)=x1-x2,即y1+y2=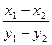 .
.
∵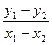 =kAB=-
=kAB=-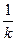 ,∴y1+y2=-k.∴
,∴y1+y2=-k.∴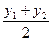 =-
=-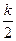 .
.
∵AB中点在直线l上,∴可得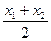 =
=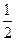 -
-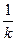 ,即弦的中点为(
,即弦的中点为(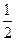 -
-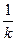 ,-
,-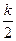 ).
).
∴由点斜式可得AB:y+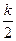 =-
=-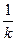 (x-
(x-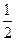 +
+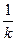 ),即x=
),即x=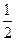 -ky-
-ky-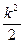 -
-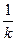 .
.
代入y2=x中得y2+ky+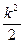 +
+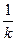 -
-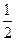 =0.
=0.
由Δ=k2-4·(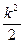 +
+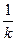 -
-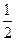 )>0,得-2<k<0即为所求.
)>0,得-2<k<0即为所求.
解法二:设抛物线上的点A(y12,y1)、B(y22,y2)关于直线l对称,则
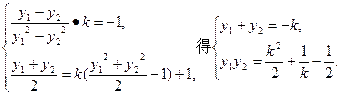
∴y1、y2是方程t2+kt+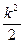 +
+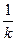 -
-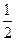 =0的两个不同根.
=0的两个不同根.
∴Δ=k2-4(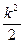 +
+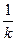 -
-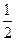 )>0,得-2<k<0即为所求.
)>0,得-2<k<0即为所求.
