问题
单项选择题
函数f(x)在[1，+∞)上具有连续导数，且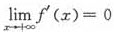
，则（）。
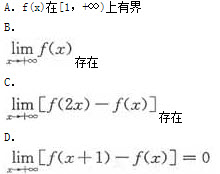
A.A
B.B
C.C
D.D
答案
参考答案：D
解析：
因为函数f(x)在[1，+∞)上具有连续导数，所以由拉格朗日中值定理可知，f(x+1)-f(x)=f’(x+δ)[(x+1)-x]=f’(x+δ)，其中0＜δ＜1。
搜题请搜索小程序“爱下问搜题”
函数f(x)在[1，+∞)上具有连续导数，且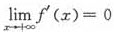，则（）。
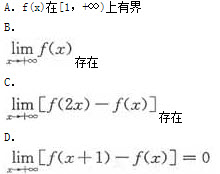
A.A
B.B
C.C
D.D
参考答案：D
解析：
因为函数f(x)在[1，+∞)上具有连续导数，所以由拉格朗日中值定理可知，f(x+1)-f(x)=f’(x+δ)[(x+1)-x]=f’(x+δ)，其中0＜δ＜1。