问题
解答题
(本小题13分)已知y=f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2-2x.
(1)求f(x)的解析式(2)作出函数f(x)的图象,并指出其单调区间.
答案
(1)当x<0时,-x>0,∴f(-x)=(-x)2-2(-x)=x2+2x,
又f(x)是定义在R上的偶函数,∴f(-x)=f(x),
∴当x<0时,f(x)=x2+2x.
f(x)=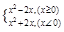
(2)由(1)知作出f(x)的图象如图所示:
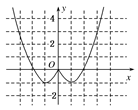
由图得函数f(x)的递减区间是(-∞,-1],[0,1].
f(x)的递增区间是[-1,0],[1,+∞).
(1)由于f(x)为偶函数,然后用-x代替x≥0时,f(x)=x2-2x中的x,f(x)不变即可得到x<0时f(x)的表达式,从而得到y=f(x)在R上的解析式.
(2)因为y=f(x)是偶函数,先作出x>0的图像,然后根据对称性再作出y轴左侧的图像.