问题
问答题
已知齐次线性方程组(Ⅰ)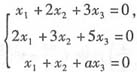 ,和(Ⅱ)
,和(Ⅱ)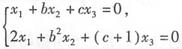 同解,求a,b,c的值.
同解,求a,b,c的值.
答案
参考答案:
根据题意可知方程组(Ⅱ)中方程组个数<未知数个数,从而(Ⅱ)必有无穷多解,所以(Ⅰ)必有无穷多解.所以(Ⅰ)的系数行列式必为0,即 a=2.
a=2.
对(Ⅰ)系数矩阵作初等变换,有 ,
,
可得方程组(Ⅰ)的通解为k(-1,-1,1)T其中k为任意常数.
由于(-1,-1,1)T是方程组(Ⅱ)的解,故有 ,
,
解得b=1,c=2,或b=0,c=1.
当b=0,c=1时,方程组(Ⅱ)为
其系数矩阵的秩为1,从而(Ⅰ)与(Ⅱ)不同解,故b=0,c=1舍去.
当a=2,b=2,c=2时(Ⅰ)与(Ⅱ)同解.
解析:
[考点] 齐次线性方程组求解