问题
问答题
设二次型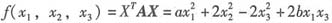 (b>0),其中二次矩阵A的特征值之和为1,特征值之积为-12.
(b>0),其中二次矩阵A的特征值之和为1,特征值之积为-12.
求a,b的值.
答案
参考答案:
由题设,二次型f相应的矩阵为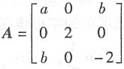 .
.
设A的3个特征值为λ1,λ2,λ3,则由已知条件知λ1+λ2+λ3=1,λ1λ2λ3=-12;利用“矩阵特征值之和=矩阵主对角线元素之和”及“特征值之积=矩阵行列式”两个关系,得a=1及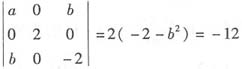 ,可求出b=2,即a=1,b=2.
,可求出b=2,即a=1,b=2.
设二次型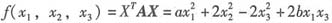 (b>0),其中二次矩阵A的特征值之和为1,特征值之积为-12.
(b>0),其中二次矩阵A的特征值之和为1,特征值之积为-12.
求a,b的值.
参考答案:
由题设,二次型f相应的矩阵为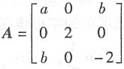 .
.
设A的3个特征值为λ1,λ2,λ3,则由已知条件知λ1+λ2+λ3=1,λ1λ2λ3=-12;利用“矩阵特征值之和=矩阵主对角线元素之和”及“特征值之积=矩阵行列式”两个关系,得a=1及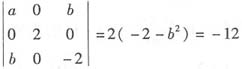 ,可求出b=2,即a=1,b=2.
,可求出b=2,即a=1,b=2.