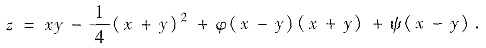问题
问答题
设z=z(x,y)有二阶连续的偏导数且满足
(Ⅰ)作自变量与因变量变换
u=x+y,v=x-y,w=xy-z,
变换z的方程为w关于u,v的偏导数满足的方程;
(Ⅱ)求z=z(x,y).
答案
参考答案:
(Ⅰ)z=xy-w,由复合函数微分法则,得
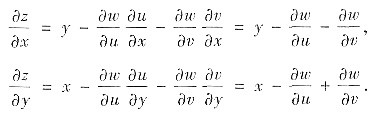
再求导
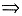
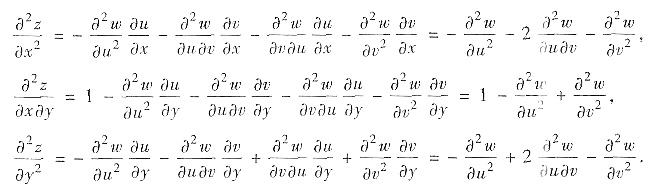
代入原方程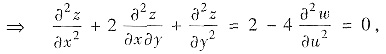
即 (*)
(*)
(Ⅱ)解方程(*),对u积分得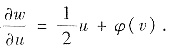 再对u积分
再对u积分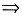
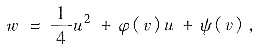
其中φ(v),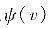 是任意的有二阶连续导数的函数,则
是任意的有二阶连续导数的函数,则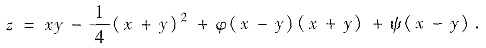
设z=z(x,y)有二阶连续的偏导数且满足
(Ⅰ)作自变量与因变量变换
u=x+y,v=x-y,w=xy-z,
变换z的方程为w关于u,v的偏导数满足的方程;
(Ⅱ)求z=z(x,y).
参考答案:
(Ⅰ)z=xy-w,由复合函数微分法则,得
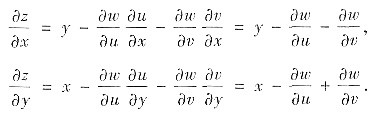
再求导

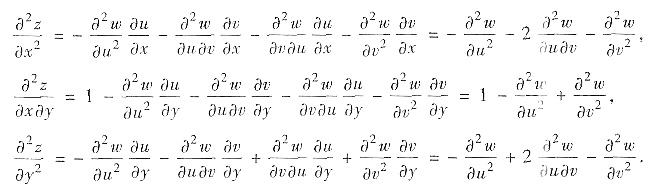
代入原方程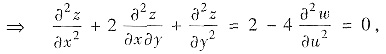
即 (*)
(*)
(Ⅱ)解方程(*),对u积分得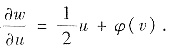 再对u积分
再对u积分
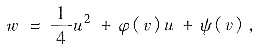
其中φ(v),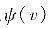 是任意的有二阶连续导数的函数,则
是任意的有二阶连续导数的函数,则