问题
问答题
设f(x)∈[a，b]，在(a，b)内二阶可导，且f"(x)≥0，φ(x)是区间[a，b]上的非负连续函数，且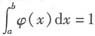
，证明：
．
答案
参考答案：
因为f"(x)≥0，所以有f(x)≥f(x0)+f’(x0)(x-x0)．
取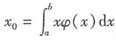
，因为φ(x)≥0，所以aφ(x)≤xφ(x)≤bφ(x)，又
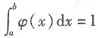，于是有
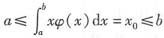，把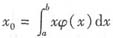
代入f(x)≥f(x0)+f’(x0)(x-x0)中，再由φ(x)≥0，得f(x)φ(x)≥f(x0)φ(x)+f’(x0)[xφ(x)-x0φ(x)]，
上述不等式两边再在区间[a，b]上积分，得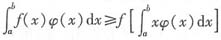
．
解析：
积分不等式的证明