问题
解答题
若f(x)=sinθcosx+(tanθ-2)sinx-sinθ是偶函数,θ为常数,且f(x)的最小值是0.
(1)求tanθ的值;
(2)求f(x)的最大值及此时x的集合.
答案
解:(1)∵f(x)是偶函数,
∴对于任意x∈R,都有f(-x)=f(x),即(tanθ-2)sinx =0,
∴tanθ=2。
(2)由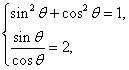 解得:
解得: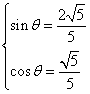 或
或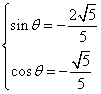 ,
,
此时,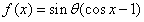 ,
,
当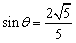 时,
时, 最大值为0,不合题意,舍去;
最大值为0,不合题意,舍去;
当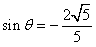 时,
时,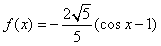 最小值为0;
最小值为0;
当cosx=-1时,f(x)有最大值为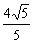 ,
,
自变量x的集合为{x|x=2kπ+π,k∈Z}.
