问题
问答题
抛物线C的方程为y=ax2(a＜0)，过抛物线C上一点P(x0，y0)(x0≠0)作斜率为k1，k2的两条直线分别交抛物线C于点A(x1，y1)，B(x2，y2)两点(P，A，B三点互不相同)，且满足k2+λk1=0(λ≠0且λ≠-1)。
(1)求抛物线C的焦点坐标和准线方程；
(2)设直线AB上一点M，满足
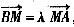，证明：线段PM的中点在y轴上。
答案
参考答案：
由抛物线C的方程y=ax2(a＜0)，得焦点坐标为
，准线方程为
(2)设直线PA的方程为y-y0=k1(x-x0)，
直线PB的方程为y—y0=k2(x-x0)。
联立方程组得
将②代入①得似ax2-k1x+k1x0-y0)=0。于是
，③
因为点P(x0，y0)和点A(x1，y1)的坐标是方程组
的解，
将⑤代入④得
由已知得
， ⑥
设点M的坐标为(xM，yM)。
将③式和⑥式代入上式得
且xM+x0=0。所以线段PM的中点在y轴上。