问题
问答题
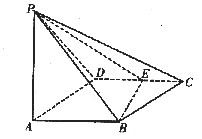
如图,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,点E是CD的中点,PA⊥底面ABCD,
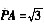 。
。
(1)求证:平面PBE⊥平面PAB:
(2)求二面角A-BE-P的大小。
答案
参考答案:
(1)如图,连接BD,
由四边形ABCD是菱形,且∠BCD=60°,
得△BCD是等边三角形。
因为点E是CD的中点,
所以BE⊥CD。
又因为AB∥CD,
所以BE⊥AB。
又因为PA⊥底面ABCD,BE⊥平面ABCD,
所以PA⊥BE。
而PA∩AB=A,
故BE⊥平面PAB。
又BE⊥平面PBE,
所以平面PBE⊥平面PAB。
(2)由(1)知BE⊥平面PAB,PB⊥平面PAB,
所以PB⊥BE。
又因为AB⊥BE,所以∠PBA是二面角A-BE-P的平面角。
在Rt△PAB中,
在Rt△PAB中,
所以,在Rt△AHG中,
故二面角A-BE-P的大小为60°。
