问题
问答题
已知A=(α1，α2，α3，α4)是4阶矩阵，α1，α2，α3，α4是4维列向量，若方程组Ax=β的通解是(1，2，2，1)T+k(1，-2，4，0)T，又B=(α3，α2，α1，β-α4)，求方程组Bx=α1-α2的通解.
答案
参考答案：由方程组Ax=β的解的结构，可知
r(A)=r(α1，α2，α3，α4)=3，
且α1+2α2+2α3+α4=β，α1-2α2+4α3=0.
因为B=(α3，α2，α1，β-α4)=(α3，α2，α1，α1+2α2+2α3)，且α1，α2，α3线性相关，而知秩r(B)=2.
由
，知(0，-1，1，0)T是方程组Bx=α1-α2的一个解.
又由
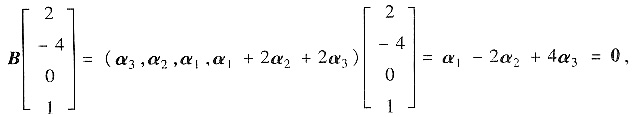
可知(4，-2，1，0)T，(2，-4，0，1)T是Bx=0的两个线性无关的解.
故Bx=α1-α2的通解是：(0，-1，1，0)T+k1(4，-2，1，0)T+k2(2，-4，0，1)T.
解析：要会正反两个方面用好方程组解的结构；要会用观察法来分析方程组的解.