证明下列命题:
(Ⅰ)设f(x,y)定义在全平面上,且
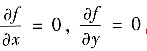 ,则f(x,y)恒为常数;
,则f(x,y)恒为常数;
(Ⅱ)设u(x,y),v(x,y)定义在全平面上,且满足
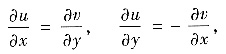 u2+v2=c(常数),
u2+v2=c(常数),
则u(x,y),v(x,y)恒为常数.
参考答案:(Ⅰ)方法1°即证f(x,y)=f(0,0)
 . 由于
. 由于
f(x,y)-f(0,0)=[f(x,y)-f(0,y)]+[f(0,y)-f(0,0)]
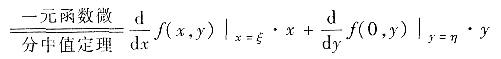
(其中ξ在x,0之间,η在0,y之间)
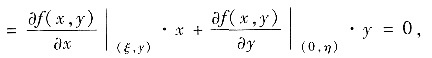
因此f(x,y)=f(0,0)
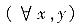 .
.
方法2°偏导数实质上是一元函数的导数,在全平面上,
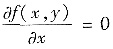 ,即
,即
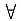 给定y,作为x的一元函数f(x,y)对x的导数
给定y,作为x的一元函数f(x,y)对x的导数
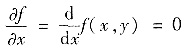
于是f(x,y)=φ(y)
φ(y)是
 可导函数(当y给定时它是x的常数函数).
可导函数(当y给定时它是x的常数函数).
将上式两端关于y求偏导数与导数,有
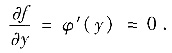
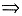
f(x,y)=φ(y)=G.
因此f(x,y)恒为常数.
(Ⅱ)由所给条件即证
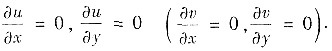
由
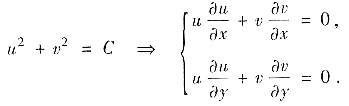
将
 代入上式
代入上式
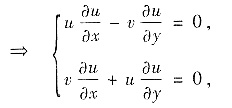
此方程组的系数行列式
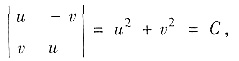
若C=0
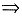 u=0,v=0;若
u=0,v=0;若
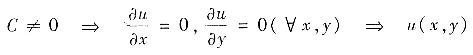 为常数.
为常数.
同理可证:v(x,y)为常数,
解析:①对于这类证明题,考生要注意题设条件与结论的内在关系及所证结论的转换. 例如:设函数z=f(x,y)具有二阶连续编导数,且
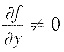 ,试证对任意的常数C,f(x,y)=C确定y=y(x)为一直线的充要条件是
,试证对任意的常数C,f(x,y)=C确定y=y(x)为一直线的充要条件是
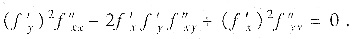
([提示]由于y=y(z)是线性函数的充要条件为y′(x)=K(K为常数),进而y″(x)=0. 设y=y(x)是由方程f(x,y)=C确定的隐函数,则只需证题中的条件是
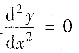 的充要条件.
的充要条件.
②作为复习,请考生证明:(Ⅰ)设u(x,y)有二阶连续偏导数,则u(x,y)=f(x)+g(y)的充要条件是
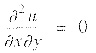 . (Ⅱ)设u(x,y)≠0,且具有二阶连续编导数,则u(x,y)=f(x)·g(y)的充分必要条件是
. (Ⅱ)设u(x,y)≠0,且具有二阶连续编导数,则u(x,y)=f(x)·g(y)的充分必要条件是
 ([提示]该题与题(Ⅰ)是相类似的问题,证明思路同题(Ⅰ)的方法2°. )
([提示]该题与题(Ⅰ)是相类似的问题,证明思路同题(Ⅰ)的方法2°. )
分析与证明:
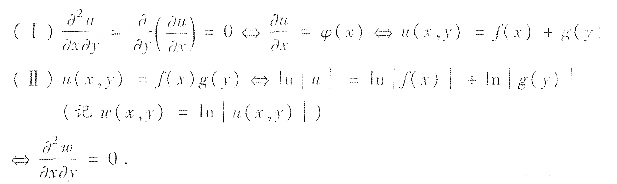
现求出

