参考答案：

因为|PF₁|，|F₁F₂|，|PF₂|成等差数列，

所以2|F₁F₂|=|PF₁|+|PF₂|。①

又因为双曲线的焦点是F₁，F₂，P是双曲线上的一点，

所以||IPF₁|-|PF₂||=4。②

①²+②²得|PF₁|²+|PF₂|²=8+8c²。③

设∠POF₁=0，∠POF₂=π-θ，

则|PF₁|²=|PO|²+|OF₁|²-2|PO||OF₁|cos0，

|PF₂|²=|PO|²+|OF₂²|²-2|PO||OF₂|cos(π-θ)，

所以|PF₁|²+|PF₂|²=2|PO|²+2c²，

联立③得2|PO|²+2c²=8+8c²，

即|PO|²=4+3c²=4+3(4+b²)=16+3b²＜25，即b²＜3.

又因为b∈N₊，所以b=1，即双曲线的方程为

。
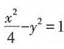