问题
问答题
已知双曲线C的中心是原点，右焦点为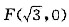
，一条渐近线m：
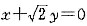，设过点A(-3
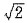，0)的直线z的方向向量
．
证明：当[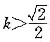
]时，在双曲线C的右支上不存在点Q，使之到直线l的距离为[
]．
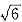答案
参考答案：
证法一：设过原点且平行于l的直线b：kx-y=0，
则直线l与b的距离
．
又双曲线C的渐近线为
．
∴双曲线C的右支在直线b的右下方，
∴双曲线C的右支上的任意点到l的距离大于
．
故在双曲线C的右支上不存在点Q，使之到直线l的距离为
．
证法二：假设双曲线C右支上存在点Q(x0，y0)到直线l的距离为
．
则
由(1)得
．
设
．
当
时，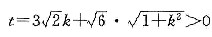
．
将y0=kx0+t代入(2)得
(*)
∵
，
∴1-2k2＜0，-4kt＜0，-2(t2+1)＜0．
∴方程(*)不存在正根，即假设不成立，
故在双曲线C的右支上不存在点Q，使之到直线的距离为
．