问题
解答题
函数f(x)=log2|x|+1，
（1）用定义证明f(x)是偶函数；
（2）解不等式：f(x)≥3。
答案
（1）证明：由条件知函数f(x)的定义域为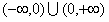
，
对于任意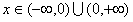
，有
，
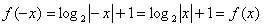所以函数f(x)为偶函数。
（2）解：即：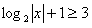
，所以，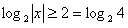
，
即|x|≥4，所以x≥4或x≤-4，
所有，原不等式的解集为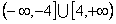
。
搜题请搜索小程序“爱下问搜题”
函数f(x)=log2|x|+1，
（1）用定义证明f(x)是偶函数；
（2）解不等式：f(x)≥3。
（1）证明：由条件知函数f(x)的定义域为，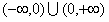
对于任意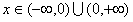，有，
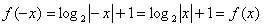所以函数f(x)为偶函数。
（2）解：即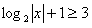：，所以，，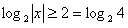
即|x|≥4，所以x≥4或x≤-4，
所有，原不等式的解集为。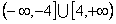
