问题
填空题
一个正方形的外接圆半径与其内切圆半径之比是______．
答案
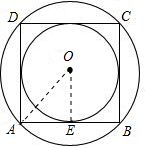
如图所示，
连接OA、OE，
∵AB是小圆的切线，
∴OE⊥AB，
∵四边形ABCD是正方形，
∴AE=OE，
∴△AOE是等腰直角三角形，
设AE=x，
则OA=
=OE2+AE2
=x2+x2
x，2
故
=OA OE
=
x2 x
．2 1
故答案为：
：1．2
搜题请搜索小程序“爱下问搜题”
一个正方形的外接圆半径与其内切圆半径之比是______．
如图所示，
连接OA、OE，
∵AB是小圆的切线，
∴OE⊥AB，
∵四边形ABCD是正方形，
∴AE=OE，
∴△AOE是等腰直角三角形，
设AE=x，
则OA=
=OE2+AE2
=x2+x2
x，2
故
=OA OE
=
x2 x
．2 1
故答案为：
：1．2