问题
选择题
设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
答案
答案:C
设M(x0,y0),A(0,2),MF的中点为N.
由y2=2px,F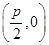 ,∴N点的坐标为
,∴N点的坐标为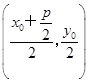 .
.
由抛物线的定义知,x0+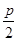 =5,∴x0=5-
=5,∴x0=5-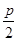 .∴y0=
.∴y0= 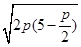 .
.
∵|AN|=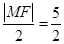 ,∴|AN|2=
,∴|AN|2=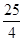 ∴
∴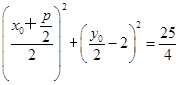 .
.
即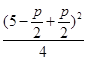 +
+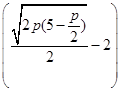 2=
2=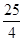 .
.
∴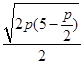 -2=0.整理得p2-10p+16=0.
-2=0.整理得p2-10p+16=0.
解得p=2或p=8.∴抛物线方程为y2=4x或y2=16x
