问题
填空题
等边三角形的内切圆半径与外接圆半径的比是______.
答案
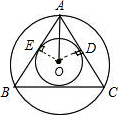
如图,连接OD、OE;
因为AB、AC切圆O与E、D,
所以OE⊥AB,OD⊥AC,
又因为AO=AO,
EO=DO,
所以△AEO≌△ADO(HL),
故∠DAO=∠EAO;
又∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠OAC=60°×
=30°,1 2
∴OD:AO=1:2.
等边三角形的内切圆半径与外接圆半径的比是1:2.
等边三角形的内切圆半径与外接圆半径的比是______.

如图,连接OD、OE;
因为AB、AC切圆O与E、D,
所以OE⊥AB,OD⊥AC,
又因为AO=AO,
EO=DO,
所以△AEO≌△ADO(HL),
故∠DAO=∠EAO;
又∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠OAC=60°×
=30°,1 2
∴OD:AO=1:2.
等边三角形的内切圆半径与外接圆半径的比是1:2.