问题
问答题
设A是n阶反对称矩阵，
(Ⅰ) 证明：A可逆的必要条件是n为偶数；当n为奇数时，A*是对称矩阵；
(Ⅱ) 举一个4阶不可逆的反对称矩阵的例子；
(Ⅲ) 证明：如果λ是A的特征值，那么-λ也必是A的特征值．
答案
参考答案：[解] (I)按反对称矩阵定义：AT=-A，那么
|A|=|AT|=|-A|=(-1)n|A|，即[1-(-1)n]|A|=0．
若n=2k+1，必有|A|=0．所以A可逆的必要条件是n为偶数．
因AT=-A，由(A*)T=(AT)*有
(A*)T=(AT)*=(-A)*．
又因(kA)*=kn-1A*，故当n=2k+1时，有
(A*)T=(-1)2kA*=A*，
即A*是对称矩阵．
(Ⅱ)例如，
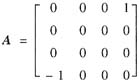是4阶反对称矩阵，且不可逆．
(Ⅲ)若A是A的特征值，有|λE-A|=0，那么
|-λE-A|=|(-λE-A)T｜=｜-λE-AT|=|-λE+A|
=|-(λE-A)|=(-1)n｜λE-A｜=0，
所以-λ是A的特征值．