问题
问答题
设总体X的概率密度为
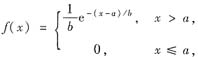
其中α，b(b＞0)都是未知参数．又X1，X2，…，Xn是取自总体X的简单随机样本，试求：
(Ⅰ) α与b的矩估计量；
(Ⅱ) α与b的最大似然估计量．
答案
参考答案：[解] (Ⅰ)
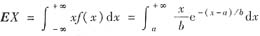
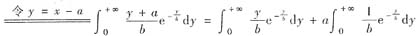
令随机变量Y服从参数λ=1／b的指数分布，概率密度记为fY(y)，由于EY=1／λ=b，DY=1／λ2=b2，于是有
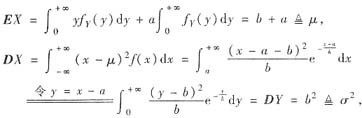
解以a，b为未知量的方程组
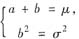可得b=σ，α=μ-σ．
于是a，b的矩估计量分别是
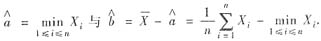
(Ⅱ)设x1，x2，…，xn为样本X1，X2，…，Xn的观测值，则似然函数L(x1，x2，…，xn；α，b)垒L(a，b)为
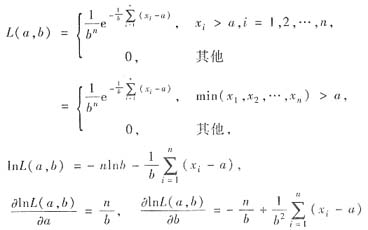
由于n/b＞0，故lnL(α，b)与L(α，b)关于α是增函数，但是又因只有α＜min(x1，x2，…，xn)时，L(α，b)才不等于零，故n可取的最大值为min(x1，x2，…，xn)．再根据方程
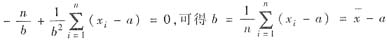
于是a，b的最大似然估计量分别为