问题
问答题
求f(x，y，z)=2x+2y-z2+5在区域Ω：x2+y2+z2≤2上的最大值与最小值．
答案
参考答案：[分析与求解] f(x，y，z)在有界闭区域Ω上连续，一定存在最大、最小值．
第一步，先求f(x，y，z)在Ω内的驻点．
由
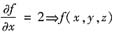在Ω内无驻点，因此，(x，y，z)在Ω的最大、最小值都只能在力的边界上达到．
第二步，求f(x，y，z)在Ω的边界x2+y2+z2=2上的最大、最小值，即求f(x，y，z)在条件x2+y2+z2-2=0下的最大、最小值．
令F(x，y，z，λ)=2x+2y-z2+5+λ(x2+y2+z2-2)，解方程组
由①，②
x=y，由③
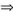z=0或λ=1．由x=y，z=0代入④
x=y=±1，z=0．当λ=1时由①，②，④也得x=y=-1，z=0．因此得驻点，P1(-1，-1，0)与P2(1，1，0)．计算得知f(P1)=1，f(P2)=9．
因此，f(x，y，z)在Ω的最大值为9，最小值为1．
