问题
填空题
已知抛物线y2＝2px，以过焦点的弦为直径的圆与抛物线准线的位置关系是________．
答案
相切
设抛物线焦点弦为AB，中点为M，准线为l，A1、B1分别为A、B在直线l上的射影，则|AA1|＝|AF|，|BB1|＝|BF|，于是M到l的距离d＝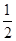
(|AA1|＋|BB1|)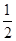＝(|AF|＋|BF|)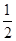＝|AB|＝半径，故相切．
搜题请搜索小程序“爱下问搜题”
已知抛物线y2＝2px，以过焦点的弦为直径的圆与抛物线准线的位置关系是________．
相切
设抛物线焦点弦为AB，中点为M，准线为l，A1、B1分别为A、B在直线l上的射影，则|AA1|＝|AF|，|BB1|＝|BF|，于是M到l的距离d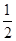＝(|AA1|＋|BB1|)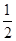＝(|AF|＋|BF|)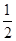＝|AB|＝半径，故相切．