问题
解答题
在平面几何中,我们可以证明:周长一定的多边形中,正多边形面积最大.使用上边的事实,解答下面的问题:
用长度分别为2、3、4、5、6(单位:cm)的五根木棒围成一个三角形(允许连接,但不允许折断),求能够围成的三角形的最大面积.
答案
因为周长一定(2+3+4+5+6=20cm)的三角形中,以正三角形的面积最大.
取三边尽量接近,使围成的三角形尽量接近正三角形,则面积最大.
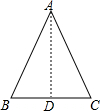
此时,三边为6、5+2、4+3,这是一个等腰三角形.
即AB=AC=7cm,BC=6cm,
∴AD=
=249-9
(cm),10
∴最大面积为:
×6×21 2
=610
(cm2).10