阅读下面短文,从短文后各题所给的四个选项(A、B、C和D)中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
The world always makes way for the dreamer.
When I was twelve years old, my father took me to see Zig Zigler. I remember sitting in that dark hall listening to Mr. Zigler 36 everyone’s spirits up to the ceiling, I 37 there feeling like I could do anything. When we got to the car, I turned to my father and said, “Dad, I want to 38 people feel like that.” My father asked me 39 I meant. “I want to be a motivational (激励人的)speaker just like Mr. Zigler,”I replied. A 40 was born.
Recently, I began seeking my dream of motivating others. 41 a four-year relationship with Fortune 100 Company 42 as a sales-trainer and ending as a regional sales manager, I left the company at the height of my 43 . Many people were 44 that I would leave after earning a six-figure income. And they asked 45 I would risk everything for a dream.
I made my 46 to start my own company and leave my secure position after 47 a regional sales meeting. The vice-president of our company delivered a 48 that changed my life. He asked us, “If a god would offer you three wishes, what would they be?” After giving us a 49 to write down the three wishes, he then asked us, “Why do you need a 50 ?” I would never forget the power I felt at that moment. I realized that 51 I had accomplished in the past had prepared me for this moment. I was ready and didn’t need a god’s help to become a motivational speaker. A motivational speaker was 52 .
Having made that decision, I was immediately 53 .One week after I gave notice, my husband was laid off from his job, and now we had no 54 . But I held fast to my dream. The wonder really began to happen. In a short time my husband found a better job.And I was able to book several 55 engagements with new customers. I discovered the incredible power of dreams.
| 小题2: | | A.slipped | B.came | C.arrived | D.left |
|
| 小题5: | | A.speaker | B.idea | C.girl | D.dream |
|
小题6:A.Because B.Before C After D.While
| 小题7: | | A.regarding | B.working | C.acting | D.beginning |
|
| 小题8: | | A.life | B.love | C.income | D.career |
|
| 小题9: | | A.surprised | B.moved | C.disappointed | D.delighte |
|
| 小题11: | | A.plan | B.decision | C.promise | D.mind |
|
| 小题12: | | A.entering | B.joining | C.attending | D.holding |
|
| 小题13: | | A.speech | B.book | C.report | D.newspaper |
|
| 小题14: | | A.day | B.second | C.week | D.moment |
|
| 小题15: | | A.help | B.god | C.job | D.company |
|
| 小题16: | | A.something | B.anything | C.nothing | D.everything |
|
| 小题17: | | A.alive | B.born | C.missing | D.dead |
|
| 小题18: | | A.tested | B.searched | C.checked | D.examined |
|
| 小题19: | | A.help | B.harm | C.income | D.money |
|
| 小题20: | | A.selling | B.speaking | C.writing | D.listening |
|
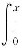 f(t)f’(2a-t)dt.证明:F(2a)-2F(a)=f2(a)-f(0)f(2a).
f(t)f’(2a-t)dt.证明:F(2a)-2F(a)=f2(a)-f(0)f(2a).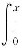 f(t)f’(2a-t)dt.证明:F(2a)-2F(a)=f2(a)-f(0)f(2a).
f(t)f’(2a-t)dt.证明:F(2a)-2F(a)=f2(a)-f(0)f(2a).