问题
填空题
设n维向量α=(a,0,…,0,a)T,a<0,E为n阶单位矩阵,矩阵A=E-ααT,B=E+
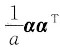 ,且B为A的逆矩阵,则a=______.
,且B为A的逆矩阵,则a=______.
答案
参考答案:-1
解析:[考点提示] 矩阵的可逆性.
[解题分析] 因为B=A-1,所以AB=E,
即
[*]
亦即
[*]
由于ααT≠0,故[*]-1-2a=0.再根据a<0,可解得a=-1.
设n维向量α=(a,0,…,0,a)T,a<0,E为n阶单位矩阵,矩阵A=E-ααT,B=E+
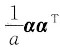 ,且B为A的逆矩阵,则a=______.
,且B为A的逆矩阵,则a=______.
参考答案:-1
解析:[考点提示] 矩阵的可逆性.
[解题分析] 因为B=A-1,所以AB=E,
即
[*]
亦即
[*]
由于ααT≠0,故[*]-1-2a=0.再根据a<0,可解得a=-1.