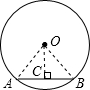
如图：

AB是半径为R的圆内接正n边形的一边，作OC⊥AB，

则∠AOC=

180°

n

，在直角△AOC中，AC=OA?sin

180°

n

，OC=OA?cos

180°

n

，

所以半径为R的圆的内接正n边形的边长为2Rsin

180°

n

，边长距为Rcos

180°

n

，

则正n边形的面积为=n?

1

2

?2Rsin

180°

n

?Rcos

180°

n

=nR²sin

180°

n

cos

180°

n

．

故答案是：nR²sin

180°

n

cos

180°

n

．