问题
选择题
过抛物线x2=2py(p>0)焦点的直线与抛物线交于不同的两点A、B，则抛物线上A、B两点处的切线斜率之积是（ ）
A.P2 B.-p2 C.－1 D.1
答案
答案：C
设A(x1,y1),B(x2,y2)
∵
=
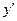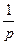x,
∴过A点的切线斜率为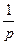x1, 过B点的切线斜率为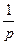x2,
∴过抛物线上A、B两点处的切线斜率之积是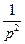
x1x2,
设过抛物线焦点的直线方程为y=kx+
与x2=2py联立消去y得
x2-2kpx-p2=0
x1x2=-p2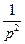x1x2=-1．