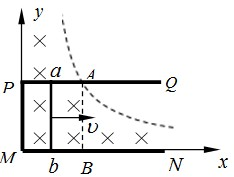
如图所示,宽度L=1.0m的光滑金属框架MNPQ固定于水平面内,以M为坐标原点,MN方向为x轴正方向建立坐标系,x、y轴与虚线所包围的有界匀强磁场磁感应强度大小B=0.5T,方向竖直向下.现将质量m=0.1kg的金属棒ab放在框架上,与y轴重合,受到F=0.7N的力作用后,由静止沿x轴方向运动,经0.5s通过AB,接着一直做a=2m/s2的匀加速直线运动.PM段电阻为1Ω,其它部分电阻不计.求
(1)金属棒ab在通过AB后0.5m的过程中,框架中产生的焦耳热
(2)金属棒ab在通过AB后0.4s时,切割磁感线产生的电动势
(3)金属棒ab在刚开始运动的0.5s内,回路中流过的电量.
(1)金属棒在匀加速的过程中,由牛顿第二定律得:F-FA=ma
求得安培力为 FA=0.5N
安培力做功为 WA=-FAx=-0.25J
故Q=-WA=0.25J
(2)令金属棒到达AB时的瞬时速度为υ1,0.4s时棒的速度为υ2,在金属棒运动到AB时,由牛顿运动定律得:F-FA=ma
F-
=maB2L2υ1 R
求得:υ1=2m/s
由运动学公式得:υ2=υ1+at=2.8m/s
此时安培力功率:P=FAυ2=0.5×2.8=1.4(W)
同时回路电功率:P=E2 R
两功率相等,可求得:E=
≈1.18(V)35 5
(3)导体棒在从y轴运动到AB的过程中,根据动量定理得:Ft-B
L•t=mυ1-0. I
又
t=q,. I
即有 Ft-BLq=mυ1
求得q=0.3C
答:(1)金属棒ab在通过AB后0.5m的过程中,框架中产生的焦耳热为0.25J.
(2)金属棒ab在通过AB后0.4s时,切割磁感线产生的电动势为1.18V.
(3)金属棒ab在刚开始运动的0.5s内,回路中流过的电量为0.3C.
