问题
问答题
设函数f(t)在(0，+∞)内具有二阶连续导数，函数
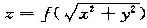满足
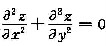，若f(1)=0，f’(1)=1，求f(x)．
答案
参考答案：[*]
由f’(1)=1得C1=1，于是[*]，故f(x)=lnx+C2，
又由f(1)=0得C2=0，故f(x)=lnx．
搜题请搜索小程序“爱下问搜题”
设函数f(t)在(0，+∞)内具有二阶连续导数，函数
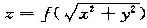满足
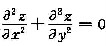，若f(1)=0，f’(1)=1，求f(x)．
参考答案：[*]
由f’(1)=1得C1=1，于是[*]，故f(x)=lnx+C2，
又由f(1)=0得C2=0，故f(x)=lnx．