问题
选择题
（5分）（2011•湖北）将两个顶点在抛物线y2=2px（p＞0）上，另一个顶点是此抛物线焦点的正三角形个数记为n，则（ ）
A．n=0
B．n=1
C．n=2
D．n≥3
答案
答案：C
题目分析：根据题意和抛物线以及正三角形的对称性，可推断出两个边的斜率，进而表示出这两条直线，每条直线与抛物线均有两个交点，焦点两侧的两交点连接，分别构成一个等边三角形．进而可知这样的三角形有2个．
解：y2=2px（P＞0）的焦点F（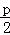
，0）
等边三角形的一个顶点位于抛物线y2=2px（P＞0）的焦点，另外两个顶点在抛物线上，则等边三角形关于x轴轴对称
两个边的斜率k=±tan30°=±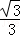
，其方程为：y=±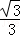（x﹣），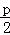
每条直线与抛物线均有两个交点，焦点两侧的两交点连接，分别构成一个等边三角形．
故n=2，
故选C
点评：本题主要考查了抛物线的简单性质．主要是利用抛物线和正三角形的对称性．
