问题
填空题
正三角形外接圆的面积是它内切圆面积的______倍.
答案
△ABC为等边三角形,AD为角平分线,⊙O为△ABC的内切圆,连OB,如图,
∵△ABC为等边三角形,⊙O为△ABC的内切圆,
∴点O为△ABC的外心,AD⊥BC,
∴∠OBC=30°,
在Rt△OBD中,OD=
OB,1 2
∴△ABC的外接圆的面积与其内切圆的面积之比=OB2:OD2=4:1.
故答案为4.
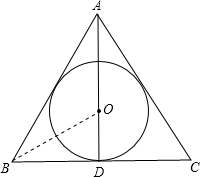
正三角形外接圆的面积是它内切圆面积的______倍.
△ABC为等边三角形,AD为角平分线,⊙O为△ABC的内切圆,连OB,如图,
∵△ABC为等边三角形,⊙O为△ABC的内切圆,
∴点O为△ABC的外心,AD⊥BC,
∴∠OBC=30°,
在Rt△OBD中,OD=
OB,1 2
∴△ABC的外接圆的面积与其内切圆的面积之比=OB2:OD2=4:1.
故答案为4.
