问题
解答题
已知直线y=-2上有一个动点Q,过点Q作直线l1垂直于x轴,动点P在l1上,且满足OP⊥OQ(O为坐标原点),记点P的轨迹为C.
(1)求曲线C的方程.
(2)若直线l2是曲线C的一条切线,当点(0,2)到直线l2的距离最短时,求直线l2的方程.
答案
(1) x2=2y(x≠0) (2) 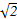 x-y-1=0或
x-y-1=0或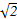 x+y+1=
x+y+1=
(1)设点P的坐标为(x,y),则点Q的坐标为(x,-2).
∵OP⊥OQ,∴当x=0时,P,O,Q三点共线,不符合题意,故x≠0.当x≠0时,得kOP·kOQ=-1,即 ·
·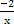 =-1,化简得x2=2y,
=-1,化简得x2=2y,
∴曲线C的方程为x2=2y(x≠0).
(2)∵直线l2与曲线C相切,∴直线l2的斜率存在.
设直线l2的方程为y=kx+b,
由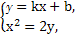 得x2-2kx-2b=0.
得x2-2kx-2b=0.
∵直线l2与曲线C相切,
∴Δ=4k2+8b=0,即b=- .
.
点(0,2)到直线l2的距离
d=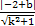 =
= ·
·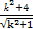
= (
(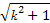 +
+ )
)
≥ ×2
×2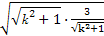
=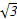 .
.
当且仅当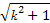 =
= ,即k=±
,即k=±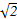 时,等号成立.此时b=-1.
时,等号成立.此时b=-1.
∴直线l2的方程为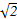 x-y-1=0或
x-y-1=0或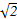 x+y+1=0.
x+y+1=0.
