问题
证明题
求证:如果函数f(x)的定义域关于原点对称,那么f(x)一定能表示成一个奇函数与一个偶函数之和。
答案
证明:∵f(x)的定义域关于原点对称,
∴f(-x),f(x)皆有意义,
又∵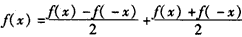 ,
,
设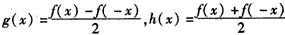 ,
,
∵g(x),h(x)的定义域都是关于原点对称的,
①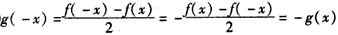 ,∴g(x)是奇函数;
,∴g(x)是奇函数;
②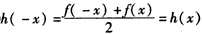 ,∴h(x)是偶函数;
,∴h(x)是偶函数;
综上可知,f(x)一定能表示成一个奇函数与一个偶函数之和.
求证:如果函数f(x)的定义域关于原点对称,那么f(x)一定能表示成一个奇函数与一个偶函数之和。
证明:∵f(x)的定义域关于原点对称,
∴f(-x),f(x)皆有意义,
又∵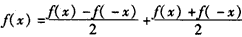 ,
,
设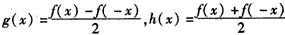 ,
,
∵g(x),h(x)的定义域都是关于原点对称的,
①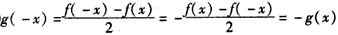 ,∴g(x)是奇函数;
,∴g(x)是奇函数;
②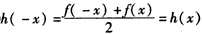 ,∴h(x)是偶函数;
,∴h(x)是偶函数;
综上可知,f(x)一定能表示成一个奇函数与一个偶函数之和.