问题
问答题
设f(x)二阶可导,且
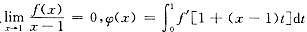 ,求
,求
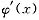 并讨论
并讨论
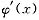 的连续性.
的连续性.
答案
参考答案:
[分析]: 首先可利用
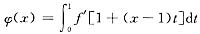 ,去掉右端积分号,将
,去掉右端积分号,将
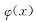 直接用f(x)表示出来,然后再求
直接用f(x)表示出来,然后再求
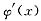 并讨论
并讨论
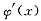 的连续性.
的连续性.
[解] 当x≠1时,令1+(x-1)t=u,
则
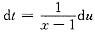
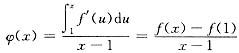
由
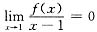 可知,f(1)=0,f′(1)=0
可知,f(1)=0,f′(1)=0
则当x≠1时,
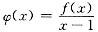
当x=1时,
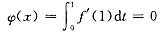
从而
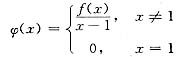
当x≠1时,
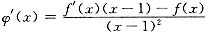
当x=1时,
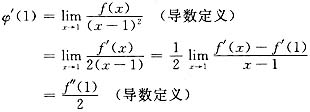
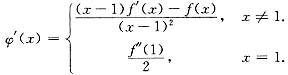
由于f(x)二阶可导,由
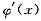 的表达A式可知,
的表达A式可知,
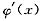 在x≠1处连续,又
在x≠1处连续,又
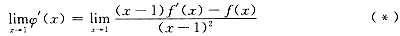
而
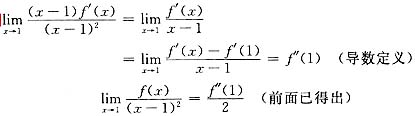
则

则
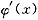 在x=1处连续,
在x=1处连续,
故
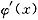 处处连续.
处处连续.
[评注] 本题是一道综合题,主要考查定积分换元法,分段函数在分界点处的连续性,可导性及洛必达法则.这里应注意,为求(*)式右端极限,这里不能用洛必达法则,也就是说以下做法是错误的.
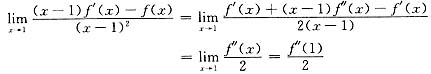
由于原题只假设f(x)二阶可导,此时极限
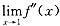 不一定存在.
不一定存在.
