问题
问答题
已知A=(α1，α2，α3，α4)是四阶矩阵，α1，α2，α3，α4是四维列向量，若方程组Ax=β的通解是(1，2，2，1)T+k(1，-2，4，0)T，又B=(α3，α2，α1，β-α4)，求方程组Bx=3α1+5α2-α3的通解．
答案
参考答案：[解] 由方程组Ax=β的解的结构，可知
r(A)=r(α1，α2，α3，α4)=3，
α1+2α2+2α3+α4=β，α1-2α2+4α3=0．
因为B=(α3，α2，α1，β-α4)=(α3，α2，α1，α1+2α2+2α3)，且α1，α2，α3线性相关，而知r(B)=2．
由
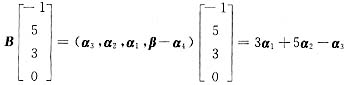，知(-1，5，3，0)T是方程组Bx=3α1+5α2-α3的一个解．
又
知(4，-2，1，0)T，(2，-4，0，1)T是Bx=0的两个线性无关的解．
故 Bx=3α1+5α2-α3的通解为
(-1，5，3，0)T+k1(4，-2，1，0)T+k2(2，-4，0，1)T，其中k1，k2是任意常数．
[评注] 本题考查抽象线性方程组的求解，涉及解的性质，解的结构，矩阵秩的判定等问题．