问题
问答题
如图所示,平板小车沿水平地面始终以加速度a做匀加速直线运动.当小车速度增至v时,将一小物块无初速地放于平板小车的A端(小车的加速度保持不变).物块与小车间的动摩擦因数为μ,(μg>a),要使物块不会从小车上滑出,求平板小车的最小长度L0.

答案
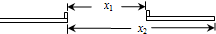
设物块的质量为m,经过时间t物块运动到小车B端,物块的末速度和位移分别为
v1=
| μmg |
| m |
x1=
| 1 |
| 2 |
| μmg |
| m |
| 1 |
| 2 |
时间t内小车的位移和末速度分别为
v2=v+at
x2=vt+
| 1 |
| 2 |
若物块刚好未从小车B端滑出,则有
v1=v2
x2=x1+L0(如图所示)
即:μgt=v+at
vt+
| 1 |
| 2 |
| 1 |
| 2 |
解得:L0=
| v2 |
| 2(μg-a) |
即平板小车的最小长度为
| v2 |
| 2(μg-a) |
