问题
问答题
设α,β为三维单位列向量,并且αTβ=0,记A=ααT+ββT,证明:
A相似于矩阵
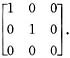
答案
参考答案:由(Ⅰ)知|A|=0,从而A有零特征值λ1=0,Ax=0的非零解x0即为λ1=0对应的特征向量。
又 Aα=(ααT+ββT)α=α(αTα)+β(βTα)=α+0=α,
Aβ=(ααT+ββT)β=α(αTβ)+β(βTβ)=0+β=β,
且α≠0,β≠0,故λ2=1为A的特征值,α,β为对应的特征向量.另外,由αTβ=0可知α,β为两个正交的非零向量,从而线性无关.所以,α,β,x0为A的3个线性无关的特征向量,λ2=1为A的2重特征值,λ1=0为A的单重特征值,记P=(α,β,x0),则[*]即A相似于矩阵[*]
