问题
问答题
已知
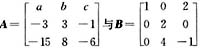 相似,试求a,b,c及可逆矩阵P,使P-1AP=B。
相似,试求a,b,c及可逆矩阵P,使P-1AP=B。
答案
参考答案:因为[*]
故B的特征值为λ1=1,λ2=2,λ3=-1,从而B可以对角化为[*]
分别求λ1,λ2,λ3所对应的特征向量,得[*]令P1=(α1,α2,α3),有[*]
由A~B得A,B有相同特征值,tr(A)=tr(B),故a+3+(-6)=1+2+(-1),即a=5.
再由|E-A|=0,|2E-A|=0得b=-2,c=2,于是
[*]
分别求A的对应于特征值1,2,-1的特征向量得[*]
令P2=(β1,β2,β3),有[*]因此
[*]
[*]
则P可逆,且P-1AP=B。
