问题
问答题
已知A,B为3阶矩阵,且满足2A-1B=B-4E,其中E是3阶单位矩阵.
(1)证明:矩阵A-2E可逆;(2)若
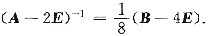 ,求矩阵A.
,求矩阵A.
答案
参考答案:[解] (1)由2A-1B=B-4E左乘A知AB-2B-4A=0.
从而(A-2E)(B-4E)=8E,或
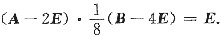
故A-2E可逆,且
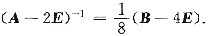
(2)由(1)知A=2E+8(B-4E)-1.
而
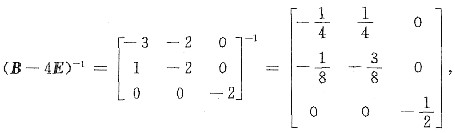
故


已知A,B为3阶矩阵,且满足2A-1B=B-4E,其中E是3阶单位矩阵.
(1)证明:矩阵A-2E可逆;(2)若
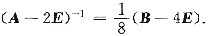 ,求矩阵A.
,求矩阵A.
参考答案:[解] (1)由2A-1B=B-4E左乘A知AB-2B-4A=0.
从而(A-2E)(B-4E)=8E,或
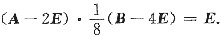
故A-2E可逆,且
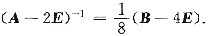
(2)由(1)知A=2E+8(B-4E)-1.
而

故

