问题
单项选择题
已知
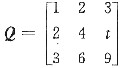，P为3阶非零矩阵，且满足PQ=0，则
(A) t=6时P的秩必为1． (B) t=6时P的秩必为2．
(C) t≠6时P的秩必为1． (D) t≠6时P的秩必为2．
答案
参考答案：C
解析： 因为P≠0，所以秩r(P)≥1，问题是r(P)究竟为1还是2
若A是m×n矩阵，B是n×s矩阵，AB=O，则r(A)+r(B)≤n．
当t=6时，r(Q)=1．于是从r(P)+r(Q)≤3得r(P)≤2．
因此(A)，(B)中对秩r(P)的判定都有可能成立，但不是必成立．所以(A)，(B)均不正确．
当t≠6时，r(Q)=2．于是从r(P)+r(Q)≤3得r(P)≤1．故应选(C)．