设A为n阶非零矩阵，A*是A的伴随矩阵，AT是A的转置矩阵，当A*=AT

问题问答题

设A为n阶非零矩阵，A^*是A的伴随矩阵，A^T是A的转置矩阵，当A^*=A^T时，证明|A|≠0．

答案

参考答案：[证法一] 由于A^*=A^T，即有A_ij=a_ij(

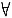i，j=1，2，…，n)，其中A_ij是行列式|A|中a_ij的代数余子式．
因为A≠0，不妨设a_ij≠0，那么

故|A|≠0．
[证法二] (反证法)若|A|=0，则AA^T=AA^*=|A|E=0．
设A的行向量为α_i(i=1，2，…，n)，则

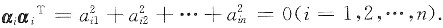
于是α_i=(α_i1，α_i2，…，α_in)=0(i=1，2，…，n)．
进而有A=O，这与A是非零矩阵相矛盾．故|A|≠0．