问题
选择题
以抛物线y2＝4x的焦点为圆心，且过坐标原点的圆的方程为( )
A．x2＋y2＋2x＝0
B．x2＋y2＋x＝0
C．x2＋y2－x＝0
D．x2＋y2－2x＝0
答案
答案：D
抛物线y2＝4x的焦点坐标为(1,0)，故以(1,0)为圆心，且过坐标原点的圆的半径为r＝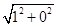
＝1，所以圆的方程为(x－1)2＋y2＝1，即x2＋y2－2x＝0．
搜题请搜索小程序“爱下问搜题”
以抛物线y2＝4x的焦点为圆心，且过坐标原点的圆的方程为( )
A．x2＋y2＋2x＝0
B．x2＋y2＋x＝0
C．x2＋y2－x＝0
D．x2＋y2－2x＝0
答案：D
抛物线y2＝4x的焦点坐标为(1,0)，故以(1,0)为圆心，且过坐标原点的圆的半径为r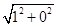＝＝1，所以圆的方程为(x－1)2＋y2＝1，即x2＋y2－2x＝0．