阅读理解。
Scientists are trying to make the deserts into good land again. They want to bring water to the deserts, so
people can live and grow food. They are learning a lot about the deserts. But more and more of the earth is
becoming desert all the time. Scientists may not be able to change the desert in time.
Why is more and more land becoming desert? Scientists think that people make deserts. People are doing
bad things to the earth.
Some places on the earth don't get much rain. But they still don't become deserts. This is because some
green plants are growing there. Small green plants and grass are very important to dry places. Plants don't let
the sun make the earth even drier. Plants do not let the wind blow the dirt away. When a bit of rain falls, the
plants hold the water. Without plants, the land can become desert more easily.
1. Deserts _____. [ ]
A. never have any plants or animals in them
B. can all be turned into good land before long
C. are becoming smaller and smaller
D. get very little rain
2. Small green plants are very important to dry places because _____. [ ]
A. they don't let the sun make the earth even drier
B. they don't let the wind blow the soil away
C. they hold water
D. All of the above
3. Land is becoming desert little by little because _____. [ ]
A. plants can't grow there
B. there is not enough rain
C. people haven't done what scientists wish them to do
D. scientists know little about the deserts
4. After reading this passage, we learn that _____. [ ]
A. plants can keep dry land from becoming desert
B. it is good to get rid of the grass in the deserts
C. all places without much rain will become deserts
D. it is better to grow crops on dry land than to cut them
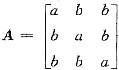 ,若A的伴随矩阵的秩等于1,则必有
,若A的伴随矩阵的秩等于1,则必有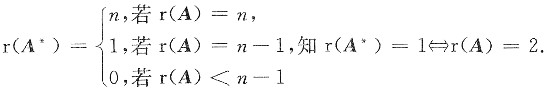
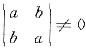 ,若r(A)=2,按定义只需|A|=0.由于
,若r(A)=2,按定义只需|A|=0.由于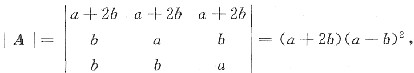
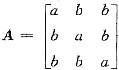 ,若A的伴随矩阵的秩等于1,则必有
,若A的伴随矩阵的秩等于1,则必有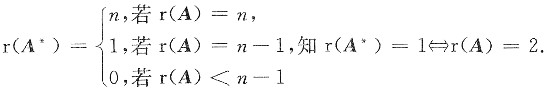
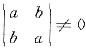 ,若r(A)=2,按定义只需|A|=0.由于
,若r(A)=2,按定义只需|A|=0.由于