问题
单项选择题
设A,B,C均为n阶矩阵,E为n阶单位矩阵,若B=E+AB,C=A+CA,则B-C=
(A) E (B) -E (C) A (D) -A
答案
参考答案:A
解析: 由
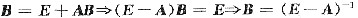
由
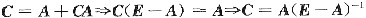
那么B-C=(E-A)-1-A(E-A)-1=(E-A)(E-A)-1=E.
故应选(A).
设A,B,C均为n阶矩阵,E为n阶单位矩阵,若B=E+AB,C=A+CA,则B-C=
(A) E (B) -E (C) A (D) -A
参考答案:A
解析: 由
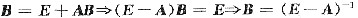
由
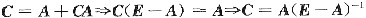
那么B-C=(E-A)-1-A(E-A)-1=(E-A)(E-A)-1=E.
故应选(A).